Компании, работающие с широкой номенклатурой, почти всегда имеют в своем ассортименте позиции, обладающие заявленной характеристикой. Важно обратить внимание на то, что речь не идет о товарах сезонного спроса. Рассматриваются позиции, по которым спрос ведет себя нестабильно в том смысле, что достаточно часто он отсутствует совсем и дело вовсе не в сезонных факторах...
С актуальностью данной проблемы мы столкнулись впервые, сотрудничая с крупным поставщиком автозапчастей. В процессе изучения ассортимента удалось выделить группу позиций, спрос на которые обладал указанным выше свойством. Типичным представителем этой группы была «рама МАЗа» - позиция дорогая, но уходящая редко и по не совсем понятному принципу. Основная проблема состояла в том, что доходность по упомянутой детали была высокой, и ее присутствие на складе было крайне желательным из соображений «ассортиментности». Но при прогнозировании продаж «рам», как, впрочем, и всех остальных позиций этой группы, оказываются неэффективными многие «традиционные» методы прогнозирования. Использование же простейших описательных статистик (минимум, максимум, среднее…) приводит к весьма ненадежным оценкам, что, в свою очередь оборачивается или отказами потенциальным покупателям, или неоправданно большими запасами. Проблема эта уже более 30-ти лет заставляет компании и аналитиков искать адекватные решения этих задач. О наиболее успешных опытах и пойдет речь ниже.
Метод Кростона и его модификация
Основная проблема при прогнозировании в данной ситуации состоит в том, что не учитывают характерную особенность рассматриваемых рядов (более 30% значений – нули) и рассматривают нулевые значения как обыкновенные наблюдения.
Еще в 1972 году Кростон предложил использовать следующий подход для решения этой проблемы:
Будем изучать два объекта: вероятность того, что спрос будет ненулевым, и величину этого ненулевого спроса. Предположим независимость событий «появление нулевого спроса» и будем моделировать вероятность этого события с помощью схемы Бернулли. Кростон также сделал еще одно существенное (и в этом – слабость модели) предположение: нормальность распределения ненулевого спроса [есть еще предпосылка о независимости и одинаковом распределении реализаций]. Таким образом, предполагается, что распределение спроса на рассматриваемую группу позиций имеет примерно следующий вид:
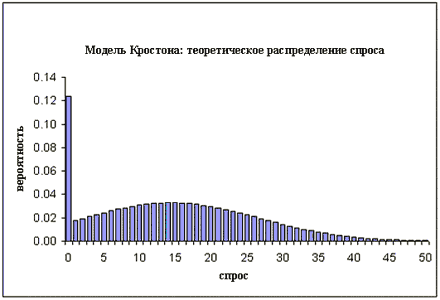
Модель Кростона: теоретическое распределение спроса
Подход Кростона предполагает оценивание трех параметров:
- Вероятность отсутствия спроса
- Средний спрос за период
- Дисперсию спроса
Первые два параметра оцениваются с помощью простого экспоненциального сглаживания, дисперсия спроса – по всем ненулевым значениям. На практике данная модель применяется, как правило, в модификации, предложенной американским математиком Виллемейном (Willemain) в 1994 году. Суть его предложения заключается в том, чтобы моделировать нормальным распределением не сами значения ненулевого спроса, а их логарифмы, что позволяет снять проблему неотрицательности изучаемых рядов.
Подход Виллемейна
Исследования 28000 временных рядов [данные были предоставлены девятью представителями европейского и американского бизнеса (авиакомпании, high tech, электроника, и т.д.)], проведенные Национальной Ассоциацией Наук (NSF) в 2002 году, позволили сделать несколько выводов по поводу эффективности применения модели Кростона для решения определенной ранее проблемы:
- Применение модели Кростона оказывается более эффективным, чем простое экспоненциальное сглаживание для прогнозирования среднего спроса за период.
- Ни экспоненциальное сглаживание, ни метод Кростона не эффективны для прогнозирования совокупного спроса за период (задача определения уровня продаж, который не будет превышен с вероятностью 95%)
Принимая во внимания указанные обстоятельства, уже упоминавшийся Виллемейн предложил следующее решение:
Допустим, мы имеем историю продаж за 2 года и хотим оценить спрос на позицию на ближайшие 3 месяца. Ниже приводится таблица с данными.
|
Для решения проблемы применяется простейшая процедура бутстрапирования:
Случайным образом выбирается три произвольных значения ежемесячного спроса (возьмем, к примеру, 4-й, 7-й и 22-й месяц, в которые было продано 0, 4 и 5 единиц товара соответственно). Рассчитывается сумма продаж (в нашем случае она равняется девяти), она запоминается и вся операция повторяется заново. После достаточно большого количества повторений таких «случайных выборов» мы получаем возможность оценить распределение совокупного спроса на продукцию и определить рациональный запас. Посмотрим на диаграмму частот, полученную в результате применения этого метода, и сравним его с диаграммой, иллюстрирующей предпосылки применения метода Кростона:
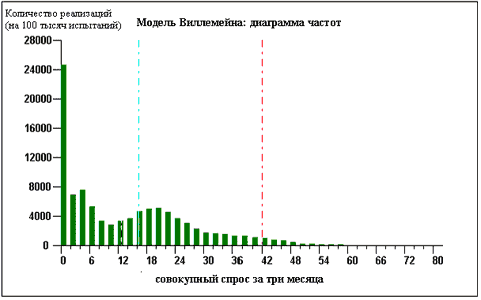
Модель Виллемейна: диаграмма частот
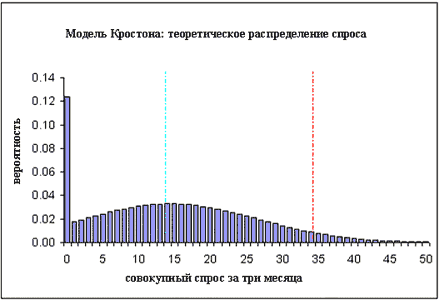
Модель Кростона: теоретическое распределение спроса
Анализируя полученные результаты, можно придти к выводу, что, моделируя спрос с помощью подхода, предложенного Кростоном, мы существенно недооценили вероятность отсутствия спроса (12 вместо 24%), а также значительно переоценили размер запаса (41 вместо 34 ед.), необходимый для того, чтобы обеспечить присутствие товара на складе в 19 случаях из 20 (правая вертикальная линия). Недооцененным в ситуации, когда применялась модель Кростона оказался и «правый хвост распределения».
Заключение
Итак, мы рассмотрели два подхода к решению первой проблемы, определили задачи, которые могут быть решены и особенности применения обоих методов. Оба метода оказываются более эффективными, чем простейший анализ диаграмм частот, однако их реализация требует наличия специализированного программного обеспечения. Заметим также, что, сталкиваясь с практическими задачами, часто встречаешь некоторый, казалось бы, «аналог» рассмотренной ситуации: ряд с большим количеством нулей, находящихся в местах, где товар отсутствовал на складе. Если оставить эту информацию без внимания, применение любых точных методов для прогнозирования соответствующих рядов становится безрезультатным: пакет сам не в состоянии будет определить, чем вызваны нулевые продажи: отсутствием спроса, или пустыми полками на складе. Таким образом, эти данные требуют предварительной обработки, которая является предметом отдельного обсуждения.